
ТЕХНИЧЕСКАЯ ИНФОРМАЦИЯ
| ФРЕЗЫ |
| СВЕРЛА |
| РЕЗЦЫ |
| МЕТЧИКИ |
| ПЛАШКИ |
| РАЗВЕРТКИ |
| ПРОТЯЖКИ |
| ЗЕНКЕРЫ |
| Резание металлов |
| ИЗМЕРЕНИЕ |
Общие сведения | Оглавление | Конструктивные особенности фасонных зуборезных фрез
Зуборезный инструмент для цилиндрических колёс
Дисковые и пальцевые зуборезные фрезы. Профилирование фасонных зуборезные фрез
Чистовые фасонные зуборезные фрезы (дисковые, пальцевые) проектируются обычно как фрезы с затылованными зубьями. У этих инструментов передний угол принимается равным нулю и передняя плоскость проходит через ось фрезы. В этом случае профиль зуба фрезы в осевом сечении будет при обработке прямозубых колес совпадать с профилем детали. Поэтому профилирование чистовых фасонных зуборезных фрез для обработки прямозубых колес заключается в определении профиля впадины зуба зубчатого колеса.
Как известно, профиль зуба эвольвентного зубчатого колеса состоит из эвольвентного участка и переходной кривой во впадине зуба.
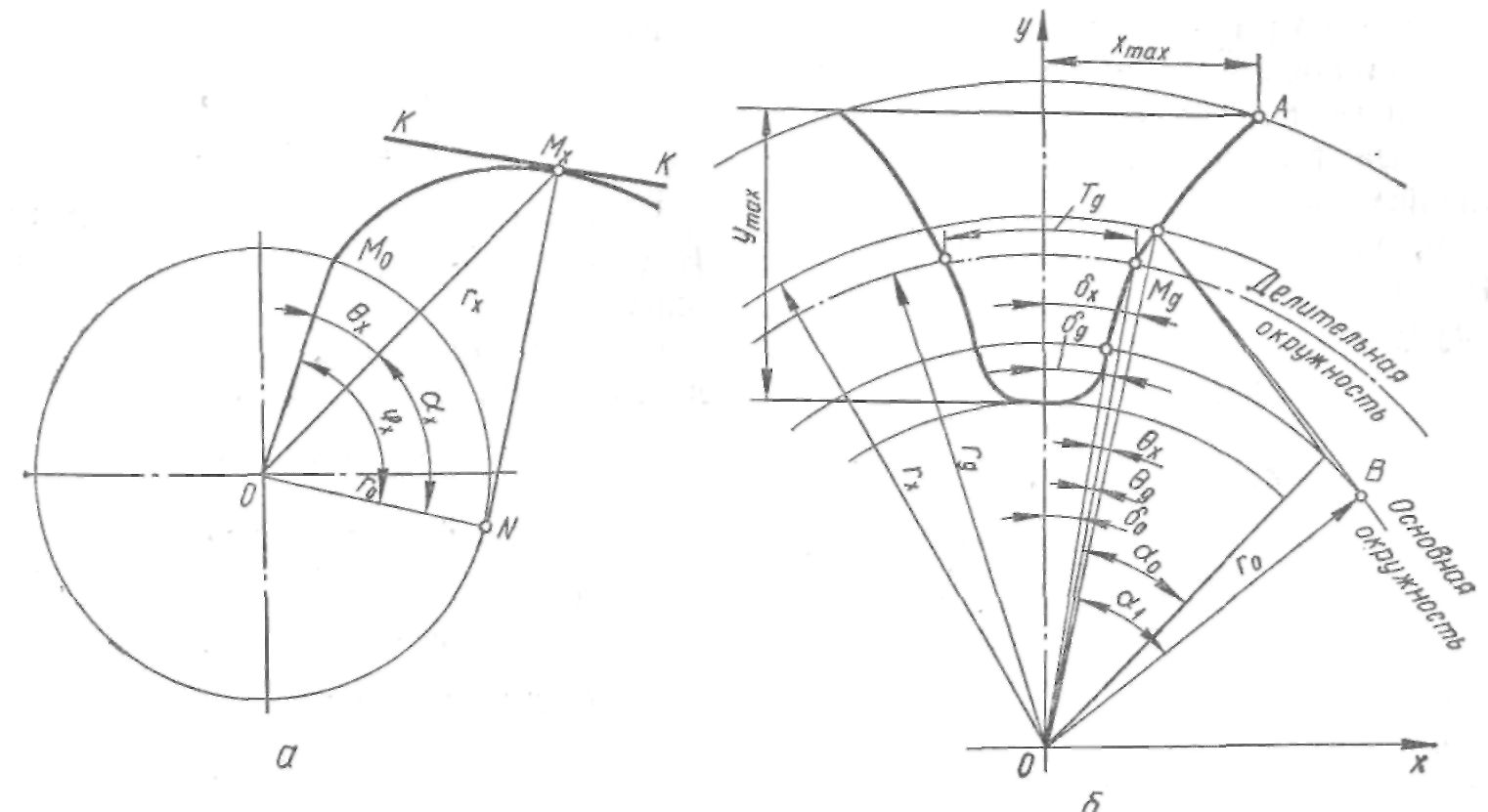 Рис. 217. Схема профилирования фасонных зуборезных фрез
Рис. 217. Схема профилирования фасонных зуборезных фрез
Эвольвентой окружности называют плоскую кривую, которая описывается любой точкой производящей прямой при ее качении без скольжения по основной окружности радиуса r0 (рис. 217, а).
Так, при качении без скольжения по окружности г0 производящей прямой точка М ее описывает эвольвенту МoMx. По построению,

Угол ФИ x, соответствующий дуге MoN, называют углом развернутости эвольвенты. Он равен
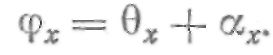
Угол ТЕТА x между радиусом МxО произвольной точки эвольвенты и радиусом МoО точки начала эвольвенты, называют эвольвентным.
Угол АЛЬФА x между радиусом 0МХ и касательной КК к эвольвенте в исследуемой точке Mx называют углом давления.
Длина дуги MoN будет равна:
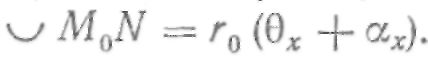
Отрезок MxN из дельтаMхON определяется таким образом:
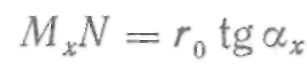
Следовательно,
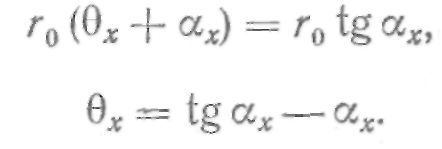
Из треугольника MхON имеем:
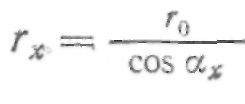
Функция tg АЛЬФА x — АЛЬФА х называется эвольвентной и обозначается inv АЛЬФА х. Для определения значения inv АЛЬФА х составлены специальные таблицы, подобные таблицам тригонометрических функций. Таким образом, уравнения эвольвенты в полярных координатах в параметрической форме будут:
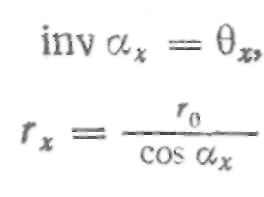
Расчет профиля впадины зуба зубчатого колеса производится по следующим известным величинам:
z— число зубьев колеса;
т — модуль;
АЛЬФА д — угол давления эвольвенты на делительной окружности;
dд — диаметр делительной окружности;
De. — диаметр окружности выступов;
di — диаметр окружности впадин;
Sд — толщина зуба колеса по делительной окружности.
Определение координат узловых точек эвольвентного профиля впадины зуба колеса будем проводить в системе ху (рис. 217, б). Начало координат системы ху поместим на оси колеса. За ось у примем ось симметрии впадины зуба зубчатого колеса. Шаг зубьев колеса на делительной окружности радиуса
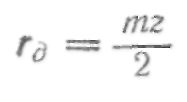
будет равен
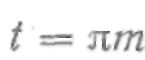
Ширина впадины зуба To на делительной окружности
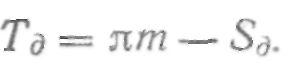
Тогда угол СИГМА д для точки Мд профиля впадины зуба, расположенной на делительной окружности, определится по формуле:
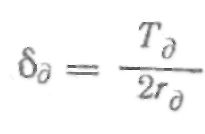
Координаты точки Мд:
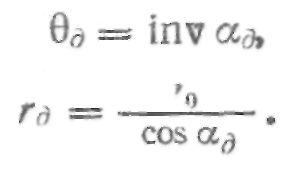
Чтобы подсчитать координаты точки В профиля, расположенной на основной окружности, запишем уравнение эвольвенты для точки Мд, расположенной на делительной окружности

Отсюда
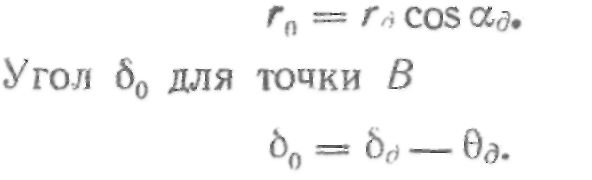
Тогда в системе ху координаты точки В начала эвольвентного профиля будут:
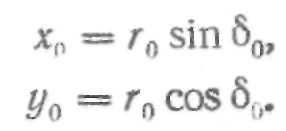
Рассмотрим произвольную точку профиля впадины зуба зубчатого колеса. Будем считать, что она расположена на известной окружности радиуса rx. Чтобы исследуемые точки располагались на реальном профиле колеса, при вычислениях необходимо радиус rx выбирать в пределах ro < rx < Re где Re — радиус окружности выступов зубчатого колеса.
Запишем уравнение эвольвенты для произвольной точки профиля впадины зуба:
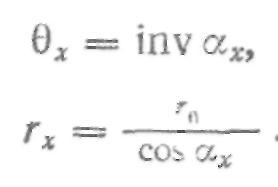
Тогда
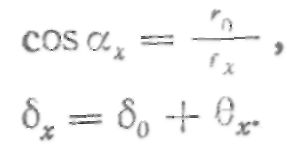
Координаты произвольной точки эвольвентного профиля впадины зуба будут:
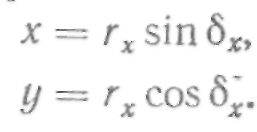
Построение профиля шаблона удобнее вести в системе хиуи, которая проводится параллельно системе ху, но смещена от начала координат вдоль оси у на расстояние, равное радиусу окружности впадины ri.
Профиль активного участка зуба колеса, на котором наблюдается соприкосновение профилей сопряженных зубьев при работе передачи, может состоять только из эвольвентной части. Этот случай имеет место при нарезании зубчатых колес с большим или средним числом зубьев, когда радиус основной окружности меньше радиуса окружности, проходящей через крайнюю точку активного участка впадины зуба обрабатываемого колеса.
Чтобы при этом обеспечить высокую прочность зуба обрабатываемого колеса, во впадине зуба создают закругление, обеспечивая плавное сопряжение активного эвольвентного участка профиля и окружности впадин. Радиус закругления выбирают таким образом, чтобы создать условия для беспрепятственного перемещения вершины зуба сопряженного колеса во впадине нарезаемого колеса.
При обработке колес с малым числом зубьев радиус основной окружности может быть больше радиуса окружности, проходящей через крайнюю точку активного участка впадины зуба.
В этом случае неэвольвентный участок профиля, расположенный между окружностью впадин и основной окружностью, оформляется в виде отрезка прямой, касательной к удлиненной эвольвенте, которую описывает вершина зуба сопряженной рейки во впадине зуба нарезаемого колеса, если неизвестно колесо, в зацеплении с которым будет работать обрабатываемое колесо.
Если же известно колесо, сопряженное с нарезаемым, то прямолинейный участок профиля проводится по касательной к удлиненной эпициклоиде, которую описывает вершина зуба сопряженного колеса во впадине обрабатываемого.
Прямолинейный участок профиля проводят под углом 5° к оси симметрии впадины зуба, благодаря чему создаются на боковых сторонах фрезы необходимые задние углы не менее 1°. Профиль впадины зуба может быть определен также графоаналитически по известному сопряженному профилю исходной зуборезной рейки.
Профиль впадины зуба зависит от числа зубьев колеса, модуля, угла профиля. Поэтому для каждого модуля, профильного угла и числа зубьев колеса теоретически необходимо иметь особую фасонную фрезу. Для уменьшения ассортимента применяют комплекты, состоящие из 8 или 15 номеров фрез определенного модуля. Каждая фреза комплекта предназначается для обработки группы колес с разным числом зубьев. Так, фреза второго номера из комплекта, включающего 8 фрез, предназначена для колес с числом зубьев, равным 14—16, а фреза седьмого номера — для колес с числом зубьев, равным 55—134. Расчет профиля фрезы ведется по колесу с наименьшим числом зубьев обрабатываемой группы колес. В результате обеспечивается меньшая опасность защемления сопряженного колеса и процесс зацепления протекает лучше, нежели при проектировании фрез по среднему или большему числу зубьев нарезаемых колес.
Общие сведения | Оглавление | Конструктивные особенности фасонных зуборезных фрез
|
ПРОДАЖА инструмента |
Copyright © 2007-2009, Фреза, сверло, метчик, плашка, развертка, резцы и другой инструмент в Москве. All rights reserved